A beautiful theory, A beautiful mind…understanding Nash Equilibrium

“If we all go for the blonde and block each other, not a single one of us is going to get her. So then we go for her friends, but they will all give us the cold shoulder because no one likes to be the second choice. But what if none of us goes for the blonde? We won’t get in each other’s way and we won’t insult the other girls. It’s the only way to win.”

This is one of the iconic scenes from the movie “A beautiful mind”. This scene shows young John Forbes Nash Jr. (played by Russell Crowe) trying to come up with the best strategy with his other friends to get a girl in a pub. This is usually taken to be an example of Nash Equilibrium and game theory in a nutshell. Well, theoretically, it does cover the concept of equilibrium, best response, and strategy. But to be precise, four mathematicians going for the blonde’s four friends is not what Nash Equilibrium strictly would be.

This article will talk about Game Theory and concepts related to it, followed by exploring and understanding the Nash Equilibrium. In the end, we’ll come back and analyze the monologue by Russel Crowe and understand its practicality considering all the topics we touch based upon.

Game Theory has been a prominent field of study for economists and mathematicians for a long time. First conceptualized by John Von Neumann in 1928, Game Theory has grown its roots in various economic theories, auction theory, strategic decision making, artificial intelligence, and even biology.

The Stanford Encyclopedia of Philosophy describes it as —

“the study of the ways in which interacting choices of economic agents produce outcomes with respect to the preferences (or utilities) of those agents, where the outcomes in question might have been intended by none of the agents.”

Sounds complicated? I agree. Here is a simplified version:

Game theory is the study of how self-interested individuals, who are trying to maximize their payoffs, strategically interact with each other. Let’s break this whole thing down into small pieces and understand the meaning of each highlighted word to make more sense out of it.

Game: A setup that includes more than one player, a set of actions each player can take, and outcomes associated with those actions.

Self-interested individuals: As the name suggests, they only care about their benefits. They are the players (i), playing the game.

Payoffs: The outcome of any action taken by a player. It can also be understood by the utility a player derives by taking a certain action.

Strategy: Choice of actions a player makes to give him/her a competitive advantage over other player/s under a given set of circumstances.

The two most popular (but not limited to) types of games in Game Theory are cooperative and non-cooperative games. Take a game where there are no conflicts of interest and all players want the same thing. For example, which side of the road should two players drive? Here, both are trying to come up with the best response so that no collision happens. This means both the players must work cooperatively. Such games are called cooperative games. Non-cooperative games on the other hand are the ones where the rational players cannot work cooperatively. Note that the word “rational player” is an assumption which means that each player is playing intending to maximize his/her payoff. A popular example of a non-cooperative game is the game of rock, paper, scissor. The most interesting games are often the ones that include both cooperation and competition. Such games cover myriads of important economic and political issues in society and are usually complex.

Before we jump into Nash Equilibrium let’s first establish an understanding of some concepts which orbit around it. To understand Nash Equilibrium, we need to understand what a Best Response is. The Best Response (BR) is an action that gives a player maximum payoff knowing what everyone else against him/her is playing. Like in the case where the players want to figure out which side to drive if one player chooses left then the other player’s best response would also be to drive left to make sure no collision happens. This means that the utility derived while taking an action (a_i) for a player i, when others take other actions (a_-i) is greater than or at least equal to any other action the player takes. This can be expressed as:

Here we denote Best Response action by (a*_i), and (Ai) is the set of all possible action player can take.

Now that we understand Best Response, let us understand what Nash Equilibrium is. Nash equilibrium is a concept which talks about the optimal outcome of a game such that none of the players have an incentive to deviate from their actions. This means all the players have come to a stable point in the game and deviating from it is not going to increase their utility further. Therefore, each player is playing the Best Response to the other’s actions. This can be expressed as:

Note that we are talking about individual actions and not strategies for all actions with varying probabilities. That is why the above is called a “pure strategy Nash Equilibrium”. In a pure strategy, a player chooses an action with 100% probability. For example, in the game of rock, paper, scissor, the player plays only one action with 100% probability at a time. In the example we discussed above regarding which side to drive, the players will maximize their payoffs driving either left or the right side of the road which would be a pure strategy Nash Equilibrium.

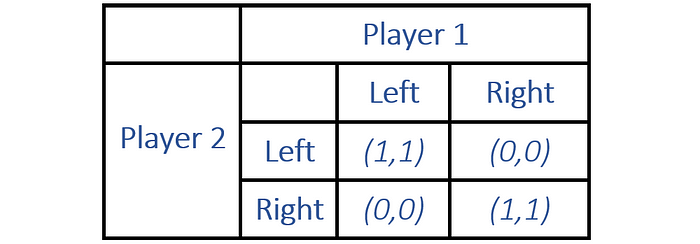
None of the players would have an incentive to deviate from their action as that would lead to a collision. Also note that a game can have more than one Nash Equilibrium (Left, Left and Right, Right).

Another form of Nash Equilibrium is called a mixed strategy Nash Equilibrium. In a mixed strategy, a player chooses various actions with varying probabilities to play in a non-deterministic way. This creates randomness so that the opponent is unable to predict the player’s next move. Mixed strategy talks about all the actions that can be taken with varying probabilities. A popular example of a mixed strategy is a penalty shootout situation in football. Neither the kicker nor the goalie can play with a pure strategy. If either of them plays with a pure strategy i.e. either kicking or saving in one direction all the time, then it would be easy for the opponent to win. Therefore, to create randomness, both of them have to play in a non-deterministic way. In real life, we often come across situations where a mixed strategy needs to be opted for. This makes the mixed strategy Nash Equilibrium important. The famous Nash theorem is also based on it. Nash theorem says:

Every finite game has at least one mixed-strategy Nash Equilibrium

A finite game is one that has — a finite number of players, a finite number of actions, and a finite number of outcomes.

Let’s come back to the “Who gets the blonde?” problem. In the scene, Nash (Russel Crowe) says that if all four mathematicians go for four of blonde’s friends, then they will not hinder each other’s path and each of them will successfully end up with a girl. There are three major assumptions taken in this situation –

1. The blonde is the most attractive among all her friends and the incentive for all four mathematicians to go for her is equal.
2. All four mathematicians have a definite and equal chance of impressing the girl they choose to approach (blonde or her friends).
3. There is no one else in the pub that would have a better chance than the four mathematicians to get the blonde or her friends.

Let’s put this in a game-theoretic framework and look at the possible outcomes. Without loss of generality, we’ll keep the four mathematicians at Princeton momentarily out of it and put ourselves in their shoes in a different situation. Imagine that you enter an auditorium with a friend where the arrangement of seats is triangular (see image below).

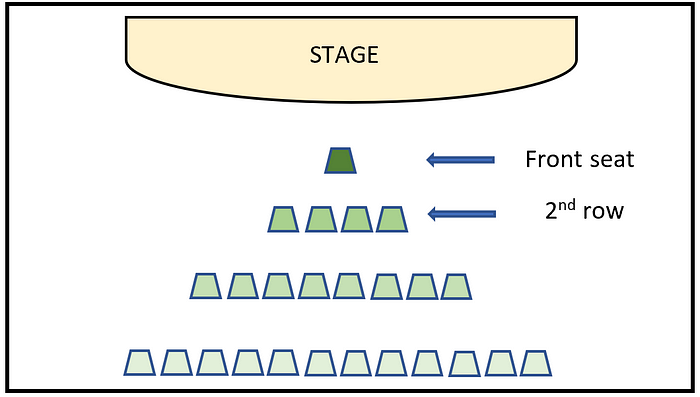
For maximizing the experience, everyone wants the front most seat close to the stage. As obvious as it can be, there can be just one person sitting on a seat. Like the blonde situation, if both of you try to get that seat, you block each other’s way, and no one gets it (Table 1). However, both of you have a definite and equal chance to grab the seat. To avoid conflict, you and your friend decide to go for the seats in the second row. Which would bring the game to a stable point where you still get a good (if not the best) experience and have a seat. Let’s see how these situations would look in the tables below:

Here 1 denotes the utility derived by taking an action to go for the seat or not. If one gets a seat, then it’s denoted by 1 otherwise 0. In the first cell of Table 2, you and your friend get a seat which is an optimal solution (1,1). But is it a Nash Equilibrium? The answer is NO. We just saw that Nash Equilibrium is a state where all the players have achieved what they want and none of them has an incentive to choose a different action because doing that will not bring any additional benefits. However, in this case, there is a good chance of either you or your friend to change your action and grab the front most seat while the other one has settled in the second row. Therefore, unless there is an agreement between both the friends that they will sit together, such a situation is likely to happen. The same is the case with the blonde situation, while other mathematicians go for the blonde’s friends, Nash or any of his friends could have deviated and gone for the blonde to get her.

John Nash’s contribution to Game Theory has brought an unimaginable and an unmatchable revolution in the way how economic agents cooperate and compete with each other on a large scale. The beauty of this theory lies in its simplicity and elegance. The foundations are simple which makes it applicable to various complex situations. The world today is obsessed with data science and machine learning. They surely are great fields to pursue and lucrative career options. However, amid these awesome fields doing wonders, there is another important science that is emerging. The science of decision making. And to be a decision scientist, the importance of knowing Game Theory could not be emphasized enough.